不同气象插值方法在新疆草地NPP估算中的可靠性评价

引用本文

任璇, 郑江华, 穆晨, 闫凯, 徐廷豹. 不同气象插值方法在新疆草地NPP估算中的可靠性评价. 草业科学, 2017,34(3):439-448
Ren Xuan, Zheng Jiang-hua, Mu Chen, Yan Kai, Xu Ting-bao. Evaluating reliability of grassland net primary productivity estimates using different meteorological interpolation methods. Pratacultural Science,2017,34(3): 439-448 复制到剪切板

Permissions

《草业科学》编辑部

不同气象插值方法在新疆草地NPP估算中的可靠性评价

任璇^1,², 郑江华^1,², 穆晨³, 闫凯³, 徐廷豹⁴

1.新疆大学资源与环境科学学院,新疆乌鲁木齐 830046

2.绿洲生态教育部重点实验室,新疆乌鲁木齐 830046

3.新疆维吾尔自治区草原总站,新疆乌鲁木齐 830046

4.澳大利亚国立大学芬纳资源与社会学院,堪培拉澳大利亚

郑江华(1973-),男,浙江江山人,教授,博士,研究方向为地理信息科学与遥感应用。E-mail:[email protected]

第一作者:任璇(1991-),女,新疆塔城人,在读硕士生,研究方向为草原生物灾害遥感监测。E-mail:[email protected]

收稿日期: 2016-08-30

基金: 新疆维吾尔族自治区草原总站委托项目(211-62207); 新疆维吾尔自治区高层次人才培养计划项目(104-40002); 教育部促进与美大地区科研合作与高层次人才培养项目(117-40101)

摘要

气象因子对研究草地生产力、植被长势、灾害评估等都有着重要的意义,本研究采用不同空间插值方法(协同克里格法Cokriging、反距离加权法IDW和ANUSPLIN法)对新疆地区90个气象站点2000-2011年多年的7月平均降水和气温数据进行空间插值分析,使用均方根误差法(RMSE)以及平均绝对误差法(MAE)对插值的结果进行评价,讨论不同方法对该地区降水和气温插值结果的影响。利用不同插值方法,基于CASA模型进行新疆草地NPP的估算,结合实测生物量数据,对3种插值方法下的估算结果进行评估,结果表明,1)降水和气温数据都是基于ANUSPLIN法的插值结果最优( MAE_降水 =6 .45, RMSE_降水 =8 .77, MAE_气温 =2 .11, RMSE_气温=3.52)。2)基于不同插值方法得到的气象要素估算的新疆草地NPP精度不同,将实测数据与同时期CASA模型模拟值相关性进行分析,基于ANUSPLIN法插值的气象要素估算NPP的精度最高( R²=0.794 7),NPP实测值与模拟值有良好的线性关系,比基于Cokriging插值的气象要素估算精度提高了13.23%,比IDW提高了20.13%。说明提高气象要素的插值精度有利于新疆草地NPP的估算研究。

关键词: 气象因子; 空间插值方法; 净初级生产力; CASA模型; ANUSPLIN

中图分类号:S812.1 文献标志码:A 文章编号:1001-0629(2017)3-0439-10 doi: 10.11829/j.issn.1001-0629.2016-0312

Evaluating reliability of grassland net primary productivity estimates using different meteorological interpolation methods

Ren Xuan^1,², Zheng Jiang-hua^1,², Mu Chen³, Yan Kai³, Xu Ting-bao⁴

1.School of Resources & Environment Science, Xinjiang University, Urumqi 830046, China;

2.Key Laboratory of Oasis Ecology, Urumqi 830046, China

3.Department of Grassland Resource, Xinjiang Uygur Autonomous Region, Urumqi 830046, China

4.Fenner School of Environment and Society, Australian National University, Canberra, Australia

Corresponding author: Zheng Jiang-hua E-mail:[email protected]

Abstract

Meteorological factors are significant in researching grassland productivity, vegetation growth, and disaster assessment. This study used different spatial interpolation methods including Cokriging (CK), inverse distance weighting (IDW), and ANUSPLIN, to analyse the average July precipitation and temperature datasets of 90 meteorological stations in Xinjiang from 2000 to 2011. In addition, the mean absolute error (MAE) and root mean square error (RMSE) were used to evaluate the interpolation results, and we discussed the effects of different interpolation methods on spatial variation of precipitation and temperature. Furthermore, the spatial variations in precipitation and temperature obtained using various interpolation methods were used to calculate the grassland net primary productivity (NPP) in Xinjiang using the Carnegie-Ames-Stanford (CASA) model and verified their accuracy using field measured biomass data. We obtained the following results, 1)The interpolation results of the precipitation and temperature using the ANUSPLIN was better than those of the other methods ( MAE_{precipitation}=6.45, RMSE_{precipitation}=8.77, and MAE_temperature=2.11, RMSE_temperature=3.52), which indicates that the ANUSPLIN is a superior method for interpolating meteorological factors in Xinjiang. 2) The accuracy of estimating the Xinjiang grassland NPP differed between the various methods. The calculation of the coefficients between the field measured biomass data and the simulated values obtained using CASA model, showed that the ANUSPLIN had the highest accuracy, with an R² of 0.794 7. There was a good linear relationship between the measured and simulated values of the grassland NPP. Compared with the Cokriging and IDW, the accuracy of ANUSPLIN was higher by 13.23% and 20.13%, respectively. These results show that improving the accuracy of the interpolation results of meteorological factors could enhance the estimation of grassland NPP.

Keyword: meteorological factors; spatial interpolation method; NPP; CASA; ANUSPLIN

Show Figures

草原作为陆地生态系统中分布最为广泛的生态系统之一, 在气候调节以及全球碳循环中起着重要作用^{[1, 2]}。净初级生产力(net primary productivity, NPP)指植物在单位时间和单位面积内积累的有机物总量, 是植物光合作用生成的有机物总量减去呼吸作用消耗之后的剩余量, 也是反映陆地生态系统响应和全球气候变化的重要参数^{[3, 4, 5, 6]}。草地NPP的研究对草地资源的合理利用, 挖掘草地气候生产潜力, 最大程度提高产量以及对草地农业生态系统中碳循环研究都具有指导意义^{[7, 8, 9, 10, 11]}。因为草原生态环境的天然脆弱性以及其对气候变化响应较为敏感, 温度和水分是影响草地生态系统演替重要气候驱动因子, 同时也是影响草地生产力的关键因素和估算草地生态环境及NPP的重要指标^{[11, 12, 13, 14]}。根据前期研究表明, 新疆草地植被NPP与降水的相关性显著^[15], 因此, 气象数据的精准性会很大程度地影响草地植被NPP的估算。

随着气候变化研究的日益深入, 如何基于有限的、分布不均的站点气象观测数据获得某一地区的气候要素时空分布情况, 从而提高降水、气温空间模拟的精度已成为气候变化领域的热点问题^{[16, 17, 18]}。空间数据的内插是由一组已知的分区数据或离散数据, 依据一定的数学关系推算未知点数据或区域数据的过程。就目前的研究方法中, 在气象要素空间插值方面, 主要使用的方法有样条法(Splines)、反距离加权法(inverse distance weight, IDW)、协同克里格插值法(Cokriging, CK)等, 气象要素的变化十分复杂, 不同的插值方法得出的结果也有很大的区别。新疆地区气象台站点分布稀疏, 且多分布于绿洲内, 周边站点较少, 空间上分布不均匀, 加之地貌复杂多样, 经纬度跨度较大, 对气象因素影响较大, 如何利用有限的站点对新疆地区气象要素空间分布进行准确模拟是一个难题。与反距离加权法、径向基函数法、协克里格方法相比, 普通克里格法对新疆全疆降水空间分布进行插值的计算精度最高^[19]。基于ANUSPLIN软件的局部薄盘光滑样条法对东北地区气温序列进行插值的结果最优^[20]。ANUSPLIN是澳大利亚科学家Hutchinson针对气候数据曲面拟合, 基于薄盘样条理论编写的专用软件, 该软件能对多个不同表面同时进行空间插值, 对不同时间段的气象数据处理, 运用ANUSPLIN尤为适合, ANUSPLIN软件已在不同国家不同领域得到了广泛运用, 并且得到了很好的评价。因此, 为了更准确地探求新疆地区降水量及气温的空间分布状况, 本研究利用ArcGIS中地统计模块对新疆地区2000-2011年降水及气温进行协同克里格插值、反距离加权插值, 并与ANUSPLIN插值结果进行对比, 以期选取适合新疆地区气象插值的模型, 提高草地NPP 估算模型精度。

1 研究区概况与研究方法

1.1 研究区概况

新疆维吾尔自治区(简称新疆)位于34° 22'-49° 33' N, 73° 32'-96° 21' E, 地处中国西北部、亚欧大陆腹地, 面积为166万km², 占中国国土面积1/6。新疆远离海洋, 四周高山环抱, 是典型的温带大陆性干旱气候, 年平均气温10.4 ℃, 年均降水量188.1 mm, 是全国降水量最少的地区之一, 且降水分布极不均匀, 北疆多于南疆, 西部多于东部, 山区多于盆地。地区温差大, 吐鲁番盆地最高温度达49.6 ℃; 北部富蕴县可可托海, 极限低温至-51.5 ℃。新疆地域辽阔, 境内既有高山、丘陵、盆地, 又有平原绿洲、戈壁和沙漠, 不同的地貌条件发育和形成了多种多样的草地类型, 新疆草地总面积约0.57亿hm², 其中可利用草地面积0.48亿hm², 占全国可利用草地面积的20.2%, 居全国第3位^{[21, 22, 23]}。

1.2 数据来源及预处理

本研究中所采用美国国家航空航天面向全球免费提供的EOS/MODIS的MOD13A1数据产品的NDVI数据(http://e4ftl01.cr.usgs.gov/MOLT/), 时间分辨率为16 d, 其中像元值采用最大合成法(maximum value composite, MVC), 空间分辨率为500 m。利用专业处理软件MRT对数据进行格式转换、投影转换、拼接, 将HDF格式转换成Tiff格式。用新疆行政区划图裁剪出新疆2000-2011年逐年7月的NDVI栅格数据。研究中使用的草地类型数据为欧盟联合研究中心(JRC)空间应用研究所(SAI)的2000年全球覆盖数据产品(GLC2000), 分辨率1 000 m。用ArcGIS提取出新疆地区高山亚高山草地、高山亚高山草甸、草甸、荒漠草地、平原草地5种类型。新疆地区DEM数据(分辨率30 m), 来源于中国科学院计算机网络信息中心国际科学数据(http://www.gscloud.cn)。

	Figure Option View Download New Window
	图1 研究区位置示意图Fig. 1 Location of study area

本研究用于空间插值的气温、降水数据来自于中国气象数据网(http://data.cma.gov.cn/), 时间序列为2000-2011年每年的7月, 包括新疆108个气象站点的气温和降水数据, 以及各个站点的经度、纬度、海拔高程。对数据进行准确性检验, 剔除不连续数据、错误数据及冗余数据, 最终用90个站点的数据进行空间插值, 在此基础上计算2000-2011年各个站点的7月平均降水量及气温。

实测数据来自新疆维吾尔自治区草原总站提供的实测生物量数据, 采集时间为2011年7月中旬, 包括荒漠草原、山地草甸、平原草原、高寒草甸、低地草甸的86个实测点。

1.3 插值方法

不同的空间插值方法, 有不同的适用范围, 针对不同数据的不同特点。在科学研究之前, 先对数据内插结果进行测试对比后, 择优选择是一般选择插值方法的原则。本研究基于2000-2011年多年7月平均降水量及气温数据, 通过对比分析协同克里格、反距离加权、ANUSPLIN插值法, 分析新疆地区最优插值方法, 借助ArcGIS软件地统计分析模块和ANUSPLIN平台实现。

1.3.1 协同克里格法(Cokriging) 协同克里格法是把区域化变量的最优估值方法从单一属性发展到两个以上的协同区域化属性。基于空间属性的相关联性, 对一个或多个变量采用空间估值的方法, 达到提高估值合理性与估值结果精度。高程数据对降水及气温有重要的影响, 所以使用高程作为影响降水和气温的第二影响因子, 加入到空间插值计算中。运用协同克里格估值方法, 其中将高程作为影响因子的公式可表示为:

Z= $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ λ _iZ_i+λ [y(x)-m_y+m_z] (1)

式中:Z表示兴趣点气温(降水)的插值结果; λ _i表示参与插值的点对预测点降水(气温)所占的权重值; n为实测站点的数量; Z_i代表第i(i=1, 2, 3, …, n)个站点的真实测量值; y(x)表示x点的高程值; m_y、m_z作为高程和降水(气温)的全局平均数值。

1.3.2 反距离加权法(IDW) 反距离加权插值是经常使用的插值方法, 即物体间的相似性与物体之间的距离呈反比。反距离加权法将样本点与插值点的距离作为权重加权平均, 样本点距离插值点越远, 权重越小, 用数学公式如下所示:

Z=[ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{1}{(d_{i}^{D})} \end{matrix}$ Z(x_i)]/[ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{1}{(d_{i}^{D})} \end{matrix}$ ] (2)

式中:Z为待估算的降水量(气温)的栅格值; Z(x_i)为第i(i=1, 2, 3, …, n)个气象站点的降水量(气温); n为用于插值的站点个数; d_i为插值点到第i个站点的距离; p为距离的幂。

1.3.3 ANUSPLIN插值法 ANUSPLIN运用普通薄盘和局部薄盘样条函数作为理论的插值方法。局部薄盘光滑样条法是在薄盘光滑样条法的基础上扩展而来, 与薄盘光滑样条法不同的是, 除普通的样条自变量以外, 局部薄盘光滑样条法允许引入线性协变量子模型, 例如海拔与气温之间的相关性^[24]。可将局部薄盘光滑样条理论模型表示为以下数学公式:

Z_i=f(x_i)+b^Ty_i+e_i(i=1, 2, …, n) (3)

式中:Z_i是i点的因变量; x_i作为d维样条的独立变量, f(x_i)为关于x需要估算的未知光滑函数; y是P维独立协变量; b为y_i的P维系数; e_i表示方差为w_iσ ²和期望值等于0的自变量随机误差; w_iσ ²中W作为权重的已知局部相对变异系数, σ ²为误差方差。当缺少b^Ty_i, 即P=0, 模型可简化为普通薄盘光滑样条, 当公式中f(x_i)不存在时, 则简化成了多元线性回归方程, 注意在局部薄盘光滑样条法中如果不存在f(x_i), 数据处理将无法进行。函数f和系数b可使用最小二乘估计法计算:

$\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} {(\frac{Z_{i} - f (x_{i}) - b^{T} y_{i}}{w_{i}})}^{2} \end{matrix}$ +ρ J_m(f) (4)

式中:ρ 为光滑参数, 数值通常大于0, 主要作用于曲面粗糙度与数据保真度之间的平衡, J_m(f)是f(x_i)的粗糙度测度函数, 作为f(x_i)的m阶偏导数。m值表示糙度次数, 在局部薄盘光滑样条法中又叫作样条次数。本研究中, 气温插值采用纬度和经度作为独立变量, 高程作为独立协变量、样条次数为3的三变量的局部薄盘光滑样条函数, 降水的空间插值由于数据范围大以及不确定性强, 所以采用平方根变换用来降低数据的值域范围, 最后再运用普通双变量的薄盘样条函数。

1.4 检验方法

为检验不同插值方法在研究区的预测精度, 利用ArcGIS地统计工具下的Subset工具随机构建两个子集, 选取90个气象站点的70%样本(N=63)为训练子集, 30%的样本(N=27)做验证子集。用训练子集中的样点进行插值预测, 得到验证子集中站点的降水(气温)值, 通过计算预测值与实测值的均方根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)作为检验插值精度的标准, 计算公式如下:

RMSE= $\begin{matrix} \sqrt[]{\frac{\overset{n}{\sum_{i = 1}} [Z^{0} (x_{i}) - Z (x_{i} {)]}^{2}}{n}} \end{matrix}$ (5)

MAE= $\begin{matrix} \frac{\overset{n}{\sum_{i = 1}} | Z^{0} (x_{i}) - Z (x_{i}) |}{n} \end{matrix}$ (6)

式中:Z⁰(x_i)与Z(x_i)分别作为第i个检验站点的预测和实测值; n为检验站点总数量。均方根误差和平均绝对误差总体数值越小, 说明插值方法的准确度越高, 平均绝对误差相同时, 均方根误差越小, 对应的准确度则越高。

1.5 草地NPP的估算

相关研究表明, CASA模型比较适用于新疆地区草地NPP估算研究^[25], 因此, 本研究采用朱文泉等^{[26, 27]}改进的CASA模型。该模型由植被所吸收的光合有效辐射(APAR)和光能转化率(ε )共同确定。公式如下:

NPP(x, t)=APAR(x, t)× ε (x, t) (7)

式中:APAR(x, t)表示在t月、在像元x处植物所吸收的光合有效辐射, ε (x, t)表示在t月、在像元x处的植物实际光能利用率。APAR由光合有效辐射的吸收占比与太阳总辐射量确定, 用以下公式计算:

APAR(x, t)=SOL(x, t)× FPAR(x, t)× 0.5 (8)

式中:SOL(x, t)表示t月x处的太阳辐射总量, 0.5通常是植物对太阳有效辐射(400-700 nm)的利用率。

光能转化率是植被把吸收的光合有效辐射(PAR)通过光合作用转化为有机碳的效率, 光能转化率受温度和水分的影响较大, 用以下公式计算:

c(x, t)=Tε ₂(x, t)× Tε ₂(x, t)× w_z(x, t)× ε _max (9)

式中:Tε ₂表示植物在不同温度条件下对光能转化率的影响, w_z表示植物在不同水分条件下对光能转化率的影响, ε _max表示在理想条件下植物的最大光能利用率。

在目前区域NPP的模型研究中, 模拟结果的检验通常采用对比法, 主要是将实测数据与模拟结果进行对比的方法。由于NPP野外实测的难度大、精度不高等因素, 所以在实际操作中一般采用将生物量转换成NPP数据用来代替NPP实测数据, 在本次研究中, 首先将生物量转换成草地NPP, 其次通过实测数据(换算值)与CASA模型模拟结果进行一对一分析, 完成模拟值的精度检验, 最后分析优化后的气象插值方法对草地NPP估算的影响。

2 结果与分析

2.1 各站点气象数据的描述性统计

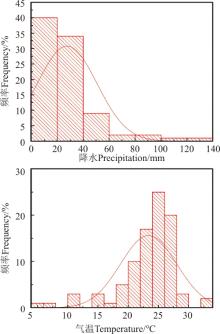
插值分析前, 对建模站点数据进行统计特征检验。2000-2011年7月平均降水量总体变化在1.77~126.04 mm, 均值为26.326 mm, 中位数与降水量平均值有一定差距, 为21.975 mm, 偏态系数为1.799 4, 呈正偏(图2)。峰度系数为6.685 9, 表明新疆地区7月降水数据的分布比标准正态分布高耸。正态分布QQ图显示, 降水数据不符合正态分布, 需进行相应的数据转换, 本研究对降水数据采用log变换进行预处理(图3)。2000-2011年7月平均气温数据总体变化在5.83~32.88 ℃, 均值为23.422 ℃, 中位数与气温平均值较接近为24.654 ℃, 偏态系数为-1.905 9, 呈负偏。峰度系数为7.907 1, 表明新疆地区7月气温数据的分布比标准正态分布高耸。正态分布QQ图显示, 数据总体倾向于正态分布, 所以对气温数据无需进行相应的数据转换。

	Figure Option View Download New Window
	图2 建模站点降水和气温数据检验分析Fig. 2 Data analysis of precipitation and temperature of modeling station

	Figure Option View Download New Window
	图3 经过log转换后的降水数据检验分析Fig. 3 Data analysis of precipitation of modeling station after log transformation

2.2 基于降水数据的不同插值方法的比较

分别以全疆90个站点多年7月平均降水量为指标, 对降水数据进行空间插值, 新疆地区降水的总体空间格局呈北高南低, 乌鲁木齐、西部的伊犁河谷等地由于受地形、海拔、地理位置等的影响, 降水量显著增加, 而在塔克拉玛干沙漠、古尔班通古特沙漠等地区降水稀少。但是, 基于Cokriging法、IDW法、ANUSPLIN法插值出的结果有一定差距(图4), 因此, 对插值结果进行验证分析, 通过计算预测值与实测值的平均绝对误差、均方根误差作为检验插值精度的标准, 可以看出, 不同插值方法之间的平均绝对误差、均方根误差并不相同(表1)。

表1 基于Cokriging, IDW和ANUSPLIN方法的误差参数比较 Table 1 Comparing error parameters of Cokriging, inverse distance weighting (IDW), and ANUSPLIN

Cokriging法与IDW法的平均绝对误差(MAE_CK=12.12, MAE_IDW=14.92)与均方根误差(RMSE_CK=21.21, RMSE_IDW=24.37)均高于ANUSPLIN法(MAE=6.45, RMSE=8.77)。ANUSPIN法精度相比较CK法提高了46.78%, 较IDW法提高了56.77%, 具有明显的优势。另外, 不同插值方法所得结果在曲线平滑程度以及局部地区的空间分布具有一定差异, ANUSPLIN法比较平滑, 更能直观地表达新疆地区降水的分布情况, 而IDW法的插值结果在部分地区形成了明显的“ 牛眼” 。综上所述, 3种插值方法在新疆地区的插值精度为ANUSPLIN> Cokriging> IDW。这说明基于ANUSPLIN软件的插值方法更加适合新疆地区的降水数据插值。

	Figure Option View Download New Window
	图4 基于不同气象插值方法的新疆地区年均7月降水量空间分布Fig. 4 Spatial distribution of annual average July precipitation of Xinjiang based on different interpolation methods

2.3 基于气温数据的不同插值方法的比较

分别利用Cokriging法、IDW法、ANUSPLIN法对新疆多年7月气温数据进行空间插值, 在南疆的沙漠地带气温较高, 尤其以吐鲁番附近气温最高, 而在一些绿洲区域及高山地区气温较低(图5)。Cokriging方法插值的气温范围为4.67~47.65 ℃, IDW方法插值的气温范围为5.83~32.59 ℃, Cokriging和IDW方法都未预测出山区的负值低温, 同时气温的地带性变异也不明显, 而ANUSPLIN则体现出了使用DEM预测气温的优势, 其插值的气温范围为-22.76~35.55 ℃。可以明显地突出昆仑山、天山、阿尔泰山的低温趋势。从平方根误差和均方根误差来看, 这3种插值方法相比较降水插值精度较高, ANUSPLIN进行的气温插值产生误差明显偏小(MAE=2.11, RMSE=3.52), 比Cokriging法(MAE=3.65, RMSE=5.28)精度提高了42.19%, 比IDW法(MAE=3.52, RMSE=4.84)精度提高了40.06%。综上所述, 3种插值方法在新疆地区插值精度为ANUSPLIN> IDW> Cokriging。说明基于ANUSPLIN软件的插值方法更加适合新疆地区的气温数据插值。

	Figure Option View Download New Window
	图5 基于不同气象插值方法的新疆地区年均7月气温空间分布Fig. 5 Spatial distribution of annual average July temperatures of Xinjiang based on different interpolation methods

2.4 基于气象数据不同插值方法对草地NPP估算的影响

新疆草地植被NPP空间分布特征受区域水热条件的制约, 空间上呈北高南低的空间格局, 最高值出现在伊犁河谷地区以及北疆地区, 最低值出现在新疆南部地区, 由于北疆雨水较多, 而南疆夏季干旱少雨, 靠近沙漠(图6)。气温、降水对于草地NPP估算是至关重要的影响因素, 因此, 提高气象因子的插值精度, 提高其估算精度, 更有利于草地NPP的研究。基于Cokriging、IDW、ANUSPLIN这3种插值方法, 对降水、气温数据进行插值, 利用CASA模型对新疆地区草地NPP进行估算, 得出3种不同插值方法下的草地NPP。结合自治区草原总站提供的实测生物量数据, 对其数据进行处理转换, 将实测数据与同时期CASA模型模拟值相关性进行分析, 在不同插值方法下的草地NPP估算精度有一定区别(图7), 其中利用ANUSPLIN法进行气象要素插值的估算精度最高(R²=0.794 7), NPP实测值与模拟值有良好的线性关系。IDW法进行气象要素插值的估算精度最低(R²=0.671 8)。利用以上3种插值方法得出草地NPP值分别与实测草地NPP值进行计算, 求出二者之间的平均绝对误差和均方根误差, 进行对比分析(表2), 从平方根误差和均方根误差来看, 利用ANUSPLIN法气象插值下估算的草地NPP精度较高(MAE=16.66, RMSE=21.23), 其精度比Cokriging法(MAE=19.20, RMSE=25.17)提高了13.23%, 比IDW法(MAE=20.86, RMSE=27.00)提高了20.13%。说明提高气象要素的插值精度有利于新疆草地NPP的估算研究。

	Figure Option View Download New Window
	图6 新疆地区草地净初级生产力(NPP)分布格局Fig. 6 Spatial distribution of mean net primary productivity (NPP) in Xinjiang grassland

	Figure Option View Download New Window
	图7 基于不同所象插值方法实测值与模拟值的对比Fig. 7 Comparison of estimated and observed results of different interpolation methods

表2 基于不同气象插值方法对估算草地NPP误差参数分析 Table 2 Estimation error of grassland net primary productivity (NPP) meteorological analysis based on different interpolation methods

3 讨论与结论

空间内插方法是气象要素区域平均过程的基础, 本研究表明, 基于ANUSPLIN插值方法的精度最高, 钱永兰等^[28]研究表明, 与反距离权重法和克里格法进行逐日气象要素插值的结果进行对比, ANUSPLIN软件的插值误差最小。

在新疆的90个气象站中分别随机选择15、30、45、60、75个站作为试验样本参与插值, 剩余的站用于检验精度, 进一步分析随着气象站密度的变化, 不同插值方法的精度变化规律。结果表明(图8), 对降水与气温数据的插值, 站台数量较少时, 对比3种插值方法, ANUSPLIN法的精度明显较高, 但提高站点数量后, 3种插值方法的精度差异逐渐减小。由此说明, 在对气象站分布不均匀且密度较低的地区的降水和气温插值时, ANUSPLIN法更有优势。

	Figure Option View Download New Window
	图8 插值精度随站台密度的变化情况Fig. 8 Variation of interpolation precision with change in station density

新疆地区地貌复杂多样, 地形起伏较大, 气象站台稀少, 且分布不均匀。因此, 利用ANUSPLIN插值方法, 考虑了地形因子对气象数据插值的影响, 消除了地形对其空间分布格局的制约。利用ANUSPLIN插值的分布图更接近实际情况, 本研究也进一步推进了ANUSPLIN插值方法在新疆地区的应用。

在草地NPP的研究中, 由于基础条件(如设备条件、气象数据等)的一些限制, 对于提高估算精度有一定的困难, 应该转变思路, 通过选择更优的理论以及研究方法, 不断优化和提高研究成果精度。利用遥感模型对草地NPP进行估算是代替大量人力、物力工作的一个重要手段, 因此, 估算模型的精度尤为重要, CASA模型是一个充分考虑环境条件和植被本身特征的光能利用率模型, 将环境变量和遥感数据、植被生理参量联系起来, 为了更精确地估算NPP, 仅仅提高气象数据插值精度是远远不够的, 在研究中仍有需要改进的地方, 如:1)遥感数据精度不够高, 采用的500 m分辨率的MODIS产品数据及1 000 m的草地类型数据, 在今后的研究中可选择时间分辨率与空间分辨率都相对较高的数据, 将用其对研究区草地NPP估算的相关参数进行修正。2)不同草地类型的一些生理参量不同, 最大光利用率等参数也和草地类型相关, 因此将草地类型结合到光能利用率模型中, 针对不同的草地类型, 模拟出不同草地类型的最大光利用率, 进一步改进模型, 使其更合理化。3)植被指数也是光能利用率模型中重要参数, 不同区域环境合适不同的植被指数, 进一步的研究中应探索不同植被指数在估算草地NPP的适用性。

本研究选择2000-2011年7月新疆地区90个气象站点的降水、气温数据, 检验数据特征后, 分别采取协同克里格法、反距离加权法、ANUSPLIN法对降水气温数据进行插值, 再利用3种不同的插值方法得到的气象数据对新疆草地NPP进行估算, 比较其估算精度, 得出以下结论:

1)ANUSPLIN方法作为目前较好的曲面插值方法之一, 符合插值曲面对平滑度以及精确度的同时要求。通过对比研究, ANUSPLIN插值方法精度最高, 所以ANUSPLIN插值方法适合新疆地区气象数据插值。

2)ANUSPLIN法充分利用经纬度、高程等影响因素对降水以及气温的影响作用, 在气象站点密度低以及受自然因素影响站点分布不均的情况下, ANUSPLIN法的优势更加明显。新疆地区气象台站稀少、分布不均匀, 海拔变化较大、各季降水量差别很大, 因此, 为了进一步提高插值精度, 除了选择适合的插值模型, 还应引用更多的影响因子, 如坡度、坡向等。

3)由研究结果表明, 基于ANUSPLIN法得到的气象要素估算NPP的精度最高(R²=0.794 7), 因此, 提高气象数据的插值精度, 有利于草地NPP的估算研究。

对于本研究来说, 继续深入研究新疆草地NPP的估算研究仍是以后研究工作的方向, 而基于CASA模型进行草地NPP的估算中影响因素有很多, 包括降水、气温、草地类型、最大光能利用率等。因此, 在提高气象数据插值精度的同时对CASA模型中的参数本地化, 使其更加适合新疆草地NPP的估算, 以提高估算精度。

参考文献

View Option

[1]	朴世龙, 方精云, 贺金生, 肖玉. 中国草地植被生物量及其空间分布格局. 植物生态学报, 2004, 28(4): 491-498. Piao S L, Fang J Y, He J S, Xiao Y. Spatial distribution of grassland biomass in china. Acta Phytoecologica Sinica, 2004, 28(4): 491-498. (in Chinese) [本文引用:1]
[2]	Haulier Y, Seabloom E W, Borer E T, Adler P B, Harpole W S, Hillebrand H, Lind E C, S Macdougall A, Stevens C J, Bakker J D, Buckley Y M, Chu C J, Collins S L, Daleo P, Damschen E I, Davies K F, Fay P A, Firn J, Gruner D S, Jin V L, Klein J A, Knops J M H, Pierre K J L, Li W, Mcculley R L, Melbourne B A, Moore J L, Halloran L R O, Prober S M, Risch A C, Sankaran M, Schuetz M, Hector A L. Eutrophication weakens stabilizing effects of diversity in natural grassland s. Nature, 2014, 508: 521-525. [本文引用:1]
[3]	陈利军, 刘高焕, 励惠国. 中国植被净第一性生产力遥感动态监测. 遥感学报, 2002, 6(2): 129-136. Chen L J, Liu G H, Li H G. Estimating net primary productivity of terrestrial vegetation in China using remote sensing. Journal of Remote Sensing, 2002, 6(2): 129-136. (in Chinese) [本文引用:1]
[4]	沃笑, 吴良材, 张继平, 张林波, 刘伟玲. 基于CASA 模型的三江源地区植被净初级生产力遥感估算研究. 干旱区资源与环境, 2014, 28(9): 45-50. Wo X, Wu L C, Zhang J P, Zhang L B, Liu W L. Estimation of net primary production in the Three-River headwater region using CASA model. Journal of Arid Land Resources and Environment, 2014, 28(9): 45-50. (in Chinese) [本文引用:1]
[5]	陈强, 陈云浩, 王萌杰, 蒋卫国, 侯鹏, 李营. 2001-2010年黄河流域生态系统植被净第一性生产力变化及气候因素驱动分析. 应用生态学报, 2014, 25(10): 2811-2818. Chen Q, Chen Y H, Wang M J, Jiang W G, Hou P, Li Y. Change of vegetation net primary productivity in Yellow River watersheds form 2001 to 2010 and its climatic driving factors analysis. Chinese Journal of Applied Ecology, 2014, 25(10): 2811-2818. (in Chinese) [本文引用:1]
[6]	张建财, 张丽, 郑艺, 田向军, 周宇. 基于LPJ模型的中亚地区植被净初级生产力与蒸散模拟. 草业科学, 2015, 32(11): 1721-1729. Zhang J C, Zhang L, Zheng Y, Tian X J, Zhou Y. Simulation of vegetation net primary productivity and evapotranspiration based on LPJ model in Central Asia. Pratacultural Science, 2015, 32(11): 1721-1729. (in Chinese) [本文引用:1]
[7]	任继周, 胡自治, 张自和, 侯扶江, 陈全功. 中国草业生态经济区初探. 草业学报, 1999, 8(1): 12-22. Ren J Z, Hu Z Z, Zhang Z H, Hou F J, Chen Q G. Apreiminary discussion on grassland ecological-economic regions in China. Acta Prataculturae Sinica, 1999, 8(1): 12-22. (in Chinese) [本文引用:1]
[8]	Tan K, Piao S L, Peng C H, Jing Y F. Satellite based estimation of biomass carbon stocks for northeast China’s forests between 1982 and 1999. Forest Ecology and Management, 2007, 240: 114-121. [本文引用:1]
[9]	张伟科, 刘玉杰, 封志明, 孙小舟. 内蒙古天然草地生产潜力及其限制性研究. 草地学报, 2008, 16(6): 572-579. Zhang W K, Liu Y J, Feng Z M, Sun X Z. A Study of rangeland productive potential and limiting factors in Inner Mongolia Autonomous Region. ActaAgrestia Sinica, 2008, 16(6): 572-579. (in Chinese) [本文引用:1]
[10]	潘竟虎, 文岩. 中国西北干旱区植被碳汇估算及其时空格局. 生态学报, 2015, 35(23): 7718-7728. Pan J H, Wen Y. Estimation and spatial-temporal characteristics of carbon sink in the arid region of northwest China. Acta Ecologica Sinica, 2015, 35(23): 7718-7728. (in Chinese) [本文引用:1]
[11]	刘海江, 尹思阳, 孙聪, 彭福利, 周澎. 2000-2010年锡林郭勒草原NPP时空变化及其气候响应. 草业科学, 2015, 32(11): 1709-1720. Liu H J, Yin S Y, Sun C, Peng F L, Zhou P. Temporal and spatial variation of net primary productivity (NPP) and its responses with climatic changes in the Xilingol grassland from 2000 to 2010Pratacuhural Science, 2015, 32(11): 1709-1720. (in Chinese) [本文引用:2]
[12]	杜加强, 舒俭民, 张林波, 郭杨. 黄河上游不同干湿气候区植被对气候变化的响应. 植物生态学报, 2011, 11: 1192-1201. Du J Q, Shu J M, Zhang L B, Guo Y. Responses of vegetation to climate change in the headwaters of China’s Yellow River Basin based on zoning of dry and wet climate. Acta Phytoecologica Sinica, 2011, 11: 1192-1201. (in Chinese) [本文引用:1]
[13]	高浩, 潘学标, 符瑜. 气候变化对内蒙古中部草原气候生产潜力的影响. 中国农业气象, 2009, 30(3): 277-282. Gao H, Pan X B, Fu Y. Influence of climate change on potential climate productivity in grassland of central Inner Mongolia. Chinese Journal of Agrometeorology, 2009, 30(3): 277-282. (in Chinese) [本文引用:1]
[14]	Xu T B, Hutchinson M F. New developments and applications in the ANUCLIM spatial climatic and bioclimatic modelling package. Environmental Modelling & Software, 2013, 40: 267-279. [本文引用:1]
[15]	任璇, 郑江华, 穆晨, 闫凯, 刘永强, 温阿敏, 杨会枫. 新疆近15年草地NPP动态变化与气象因子的相关性研究. 生态科学, 出版中. Ren X, Zheng J H, Mu C, Yan K, Liu Y Q, Wen A M, Yang H F. Correlation analysis of the apatial-temporal variation of grassland net primary productivity and climate factors in Xinjiang in the past 15 years. Ecologic Science, in publication. (in Chinese) [本文引用:1]
[16]	殷刚, 陈曦, 塔西甫拉提·特依拜, 邵华, 白磊, 胡增运, 张弛, 徐婷. 气候模式同站点插值外推气象数据的比较. 地理研究, 2015, 34(4): 631-643. Yin G, Chen X, Tiyip·Tashpolat, Shao H, Bai L, Hu Z Y, Zhang C, Xu T. A comparison study between site-extrapolation-based and regional climate model-simulated climate datasets. Geographical Research, 201, 34(4): 631-643. (in Chinese) [本文引用:1]
[17]	王丽娜. 气象要素空间插值算法的研究及其应用. 重庆: 重庆理工大学硕士学位论文, 2014. Wang L N. Algorithm research and application of meteorological spatial interpolation. Master’s Thesis. Chongqing: Chongqing University of Technology, 2014. (in Chinese) [本文引用:1]
[18]	Tang L, Su X D, Shao G F, Zhang H, Zhao J Z. A Clustering-Assisted Regression (CAR) approach for developing spatial climate data sets in China. Environmental Modelling & Software, 2012, 38: 122-128. [本文引用:1]
[19]	王智, 吴友均, 梁凤超, 常顺利, 师庆东. 新疆地区年降水量的空间插值方法研究. 中国农业气象, 2011(3): 331-337. Wang Z, Wu Y J, Liang F C, Chang S L, Shi Q D. Study on spatial interpolation method of annual precipitation in Xinjiang. Chinese Journal of Agrometeorology, 2011(3): 331-337. (in Chinese) [本文引用:1]
[20]	陈思宁, 郭军. 不同空间插值方法在区域气温序列中的应用评估: 以东北地区为例. 中国农业气象, 2015(2): 234-241. Chen S N, Guo J. Evaluation of different spatial interpolation methods in sequence: A case study in northeast regional temperature China. Chinese Journal of Agrometeorolog, 2015(2): 234-241. (in Chinese) [本文引用:1]
[21]	高健. 新疆方志文献研究. 南京: 南京师范大学博士学位论文, 2014. Gao J. Xinjiang records documents. PhD Thesis. Nanjing: Nanjing Normal University, 2014. (in Chinese) [本文引用:1]
[22]	新疆维吾尔自治区畜牧厅. 新疆草地资源及其利用. 乌鲁木齐: 新疆科技卫生出版社, 1993. [本文引用:1]
[23]	李建龙. 新疆草地退化现状、原因及其防治对策. 中国草地, 1992(3): 17-21. Li J L. The present situation and reasons of grassland degradation in Xinjiang province and our management. Grassland of China, 1992(3): 17-21. (in Chinese) [本文引用:1]
[24]	刘志红, Tim R. McVicar, Tom G. Van Nie, 杨勤科, 李锐, 穆兴民. 基于ANUSPLIN的时间序列气象要素空间插值. 西北农林科技大学学报: 自然科学版, 2008(10): 227-234. Liu Z H, Tim R. McVicar, Tom G. VanNieYang Q K, Li R, Mu X M. Interpolation for time series of meteorological variables using ANUSPLIN. Journal of Northwest A & F University: Natural Science Edition, 2008(10): 227-234. (in Chinese) [本文引用:1]
[25]	杨红飞, 刚成诚, 穆少杰, 章超斌, 周伟, 李建龙. 近10年新疆草地生态系统净初级生产力及其时空格局变化研究. 草业学报, 2014, 23(3): 39-50. Yang H F, Gang C C, Mu S J, Zhang C B, Zhou W, Li J L. Analysis of the spatio-temporal variation in net primary productivity of grassland during the past 10 years in Xinjiang. Acta Prataculturae Sinica, 2014, 23(3): 39-50. (in Chinese) [本文引用:1]
[26]	朱文泉. 中国陆地生态系统植被净初级生产力遥感估算及其与气候变化关系研究. 北京: 北京师范大学博士学位论文, 2005. Zhu W Q. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing and its relationship with global climate change. PhD Thesis. Beijing: Beijing Normal University, 2005. (in Chinese) [本文引用:1]
[27]	朱文泉, 潘耀忠, 张锦水. 中国陆地植被净初级生产力遥感估算. 植物生态学报, 2007, 31(3): 413-424. Zhu W Q, Pan Y Z, Zhang J S. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. Acta Phytoecologica Sinica, 2007, 31(3): 413-424. (in Chinese) [本文引用:1]
[28]	钱永兰, 吕厚荃, 张艳红. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估. 气象与环境学报, 2010, 26(2): 7-15. Qian Y L, Lyu H Q, Zhang Y H. Application and assessment of spatial interpolation method on daily meteorotogica1 elements based on ANUSPLN software. Journal of Meteorology and Environment, 2010, 26(2): 7-15. (in Chinese) [本文引用:1]

2004

0.0

朴世龙, 方精云, 贺金生, 肖玉. 中国草地植被生物量及其空间分布格局. 植物生态学报, 2004, 28(4): 491-498.

Piao S

, Fang J

, He J

, Xiao

Spatial distribution of grassland biomass in china.

Acta Phytoecologica Sinica, 2004, 28(4): 491-498. (in Chinese)

Estimating carbon storage in terrestrial ecosystems has been a central focus of research over the past two decades because of its importance to terrestrial carbon cycles and ecosystem processes. As one of the most widespread ecosystem types, China’s grasslands play an important role in global change research. The grasslands in China, which are distributed primarily throughout the temperate regions and on the Tibetan Plateau, were classified into 17 community types. In the present study, a statistical model was established to estimate grassland biomass and its geographical distribution in China based on a grassland inventory data set and remote sensing data (Normalized Difference Vegetation Index) using GIS and RS techniques. We found that there was a significant correlation between aboveground biomass density and the maximum annual NDVI when expressed as a power function (R2=0.71, p<0.001). The aboveground biomass was estimated to be 146.16 TgC (1Tg=1012 g) and belowground biomass was estimated as 898.60 TgC (6.15 times of the above biomass) for a total biomass of 1 044.76 TgC. This value accounts for about 2.1%-3.7% of the world’s grassland biomass. The grassland biomass is distributed primarily in the arid and semiarid regions of Northern China and the Qinghai-Xizang Plateau. The average biomass density of China’s grasslands was 315.24 gC·m-2, smaller than the world average. The aboveground biomass density decreases from southeastern China toward the northwest corresponding with changes in precipitation and temperature. Furthermore, aboveground biomass density reached the lowest levels at 1 350 m elevation and peak levels at 3 750 m above sea level which most likely is related to China’s three-step topographical background. The ratio of total biomass of grassland to forest biomass in China is 1/4, much higher than that of the world, suggesting a greater contribution of grasslands to China’s carbon pool.

草地生态系统是陆地生态系统分布最广的生态系统类型之一，它在全球变化中的作用越来越受到重视。利用中国草地资源清查资料，并结合同期的遥感影像，建立了基于最新修正的归一化植被指数(NDVI)的我国草地植被生物量估测模型，并利用该模型研究了我国草地植被生物量及其空间分布特征。结果表明：草地植被地上生物量与当年最大NDVI值具有很好的相关关系，两者可以用幂函数很好地拟合(R2=0.71, p<0.001)。我国草地植被总地上生物量为146.16 TgC(1 Tg=1012 g)，主要集中在北方干旱、半干旱地区和青藏高原；总地下生物量为898.60 TgC，是地上生物量的6.15倍；而总生物量是1 044.76 TgC，占世界草地植被的2.1%～3.7%，其平均密度约等于315.24 gC·m-2，低于世界平均水平。我国草地植被单位面积地上生物量水平分布趋势为：东南地区高，西北地区低，与水热条件的分布趋势一致；从垂直分布看，在海拔1 350 m和3 750 m处分别出现了波谷和波峰，与我国特有的三级阶梯地势有着密切的关系。此外，我国草地植被生物量为森林的1/4左右，显著大于世界平均水平，说明我国草地在碳平衡中的贡献相对较大。

... 草原作为陆地生态系统中分布最为广泛的生态系统之一,在气候调节以及全球碳循环中起着重要作用^[1,2] ...

2014

0.0

... 草原作为陆地生态系统中分布最为广泛的生态系统之一,在气候调节以及全球碳循环中起着重要作用^[1,2] ...

2002

0.0

陈利军, 刘高焕, 励惠国. 中国植被净第一性生产力遥感动态监测. 遥感学报, 2002, 6(2): 129-136.

Chen L

, Liu G

, Li H

Estimating net primary productivity of terrestrial vegetation in China using remote sensing.

Journal of Remote Sensing, 2002, 6(2): 129-136. (in Chinese)

By means of Remote Sensing,the estimation of biomass and NPP mainly is on the basis of the models of solar energy efficiency,The biomass and NPP can be calculated through the relation among NPP,APAR and the rate(ε)of which transform APAR to the organic matter.The model is::NPP =(FPAR×PAR)× [ε ×σT×σE×σS× (1-Ym)× (1-Yg) ]On the basisof RS and GIS,the net primary production of terrestrial vegetation of China in every ten days using the NOAA AVHRR data with five channels and 8km*8km resolution cell was calculated.And then the annual NPP was accumulated.The result shows the total NPP of terrestrial vegetation of China is 6.13×10 9t/a in 1990 and the maximum NPP is 1812 9gC/m2. According to this result,the spatial distribution of NPP show a decreasing trend from soucheas China to north-west China.The distribution may have close relationship with the distribution of vegetation.The NPP varies with the different vegetation.It is indicated theat the NPP of conifer,broadleaf,shrubbry,grassland,meadow/morass,desert,and corn are 1031.92gC/m2,1023.60gC/m2,822.99gC/m2,502.10gC/m2,690.86gC/m2,132.21gC/m2 and 891.18gC/m2respectively.According to the yearly NPP,the NPP of shrubbery is 1621.07*10 6tCaˉｔ accounting for the largest part of China (16.4%)。The sequences of the other vegetation types are forest and com,grassland,meadow and desert.The yearky NPP of them are 1490.28*10 6tCaˉ1（24.3%）,1485.54*10 6tCaˉ1（24.2%），722.83*10 6tCaˉ1（11.8%），566.13*10 6tCaˉ1（9.2%）and 216.13*10 6tCaˉ1（3.52%）respectively.The NPP of differernt land use typed shows that the NPP of forest,agriculture land,grassland,water area,inhabitant aera,wasteland and hard-using land are 966.08gC/m2,897.15gC/m2,545.92gC/m2，656.28gC/m2,550.46gC/m2,299.74gC/m2 and 106.56gC/m2.According to the yearly NPP,the NPP of forest is 2096.87*10 6tCaˉ1 accounting for the largest part of China (34.2%).The sequences of the other vegetation types are grassland,agriculture land,wasteland,hard-using land,water area and inhabitant area,The yearly NPP of them are 1911.41*10 6tCaˉ1（31.2%),1760.57*10 6tCaˉ1（28.7%）,193.96*10 6tCaˉ1,125.92*10 6tCaˉ1,51.62*10 6tCaˉ1 and 3.84*10 6tCaˉ1 respectively.

植被净第一性生产力 (NPP)研究方法很多 ,运用NOAAAVHRR的可见光、近红外和热红外波段来提取和反演地面参数 ,进而准确估算陆地植被净第一性生产力 ,是一种全新的研究手段。利用遥感数据进行生物量和净第一性生产力的估算 ,主要是采用光能利用率模型 ,即通过NPP与植物吸收的光合有效辐射 (A PAR)和植被将所吸收的光合有效辐射转化为有机物的转化率 (ε)的关系来实现的。用数学公式可表达为 :NPP =(FPAR×PAR)× [ε ×σT×σE×σS× (1-Ym)× (1-Yg) ]在遥感和地理信息系统技术的支持下 ,以 1990年每旬的 8km分辨率的NOAAAVHRR 1― 5通道的影像为数据源 ,对中国每旬的陆地植被净第一性生产力进行估算 ,然后累加得出全年的NPP值。估算结果 :1990年我国陆地植被NPP总量为6.13×10 9t/a ,NPP最高值为 1812 9gC/m2 。就计算结果 ,对中国大陆植被NPP的分布规律进行了分析。遥感模型能够以面代点 ,比较真实地反映陆地植被NPP的时空分布状况 ,与我国植被分布的地理规律性相符 ,这是其它统计模型所无法比拟的

... 净初级生产力(net primary productivity,NPP)指植物在单位时间和单位面积内积累的有机物总量,是植物光合作用生成的有机物总量减去呼吸作用消耗之后的剩余量,也是反映陆地生态系统响应和全球气候变化的重要参数^[3,4,5,6] ...

2014

0.0

沃笑, 吴良材, 张继平, 张林波, 刘伟玲. 基于CASA 模型的三江源地区植被净初级生产力遥感估算研究. 干旱区资源与环境, 2014, 28(9): 45-50.

, Wu L

, Zhang J

, Zhang L

, Liu W

Estimation of net primary production in the Three-River headwater region using CASA model.

Journal of Arid Land Resources and Environment, 2014, 28(9): 45-50. (in Chinese)

以改进后的CASA模型为基础,利用MODIS数据、气象数据和植被类型数据,估算了2010年三江源地区植被净初级生产力(NPP)。结果表明:三江源地区NPP的总值为52.146×1012gC·a-1,平均值为146.66g C·m-2·a-1,呈现由东南向西北逐渐递减的空间分布趋势,并随着海拔和坡度的增高,NPP先升高后降低。

2014

0.0

陈强, 陈云浩, 王萌杰, 蒋卫国, 侯鹏, 李营. 2001-2010年黄河流域生态系统植被净第一性生产力变化及气候因素驱动分析. 应用生态学报, 2014, 25(10): 2811-2818.

Chen

, Chen Y

, Wang M

, Jiang W

, Hou

, Li

Change of vegetation net primary productivity in Yellow River watersheds form 2001 to 2010 and its climatic driving factors analysis.

Chinese Journal of Applied Ecology, 2014, 25(10): 2811-2818. (in Chinese)

基于modis-ndvi遥感数据，利用casa模型分析黄河流域2001—2010年植被净第一性生产力（npp）的空间分布格局，并结合同期气温和降水量数据，分别从不同空间和时间尺度上分析了黄河流域6种生态系统类型区域植被npp的变化趋势，并对其与气候因素的相关关系进行分析.结果表明：植被npp空间分布呈西北低、东南高的分布特征，平均npp年总量为108.53tgc，植被npp的分布与生态系统类型呈现较高的相关性；2001—2010年，植被npp总体呈上升趋势但波动较大，55.4%的面积呈现增加趋势，不同生态系统类型区域呈现不同的变化趋势；在年际水平上，黄河流域植被npp变化与气候因素没有显著相关性，但在月际水平上呈现了较高的相关性，降水量和气温对植被npp变化的影响作用相当；不同生态系统类型对气候因素呈现不同的相关性质以及时滞效应，草地对降水量的响应存在一定程度的时滞效应，荒漠对气温存在时滞效应.？

2015

0.0

张建财, 张丽, 郑艺, 田向军, 周宇. 基于LPJ模型的中亚地区植被净初级生产力与蒸散模拟. 草业科学, 2015, 32(11): 1721-1729.

Zhang J

, Zhang

, Zheng

, Tian X

, Zhou

Simulation of vegetation net primary productivity and evapotranspiration based on LPJ model in Central Asia.

Pratacultural Science, 2015, 32(11): 1721-1729. (in Chinese)

Central Asia is one of the most sensitive regions to climate changes in the world and the ecological environment is very fragile. The two main vegetation types, grasslands and croplands, are very easily influenced by water shortages and humans activities. Study on changes of net primary productivity (NPP) and evapotranspiration(ET), and their relationship with climate are important in Central Asia. In the present study, the spatio-temporal patterns and changes of NPP and ET in Central Asia (1982-2012) were analyzed based on LPJ model. The results indicated that the spatial distributions of NPP and ET were very consistent. The high-values were mainly located in forests, the mixed area of grass-forest and croplands, whereas the low-values were mainly concentrated in sparse vegetated area around the desert and grasslands of central Kazakhstan. The annual NPP and ET showed a fluctuated increasing trend. Annual NPP varied from 469.59 Tg C·a -1 to 1 130.26 Tg C·a -1 with mean of 737.24 Tg C·a -1 (185.57 g C·m -2 ·a -1 ). Annual ET varied from 695.53 km 3 ·a -1 to 1 047.69 km 3 ·a -1 with mean of 850.46 km 3 ·a -1 (214.07 mm·a -1 ). The main climate factor influencing the variations of NPP and ET was precipitation in Central Asia, while temperature played less important role in the region. The vegetation productivity of Kyrgyzstan and Tajikistan increased at a faster rate, yet Turkmenistan indicated a decline trend. Kazakhstan, Uzbekistan and Xinjiang’s vegetation productivitywere relatively stable.

中亚干旱区是对全球气候变化最敏感的区域之一,以草地和耕地为主的植被类型极易受到水资源短缺和人为等因素影响,导致生态环境极易恶化,故分析其植被净初级生产力(NPP)和蒸散(ET)变化特征及对气候的响应具有重要意义。本研究利用LPJ模型模拟中亚地区1982-2012年NPP和ET,并分析其在中亚潜在植被类型中的空间分布和变化特征。结果表明,1)NPP和ET的高低值空间分布基本一致,高值区主要分布在林地、草林地混合区以及耕地区,低值区主要分布在植被稀少的荒漠周边区域和哈萨克中部草地区;2)NPP总量和ET总量均呈波动上升趋势,其中NPP年度变化范围在469.59~1 130.26 Tg C·a -1 ,年均值为737.24 Tg C·a -1 (185.57 g C·m -2 ·a -1 ),ET范围在695.53~1 047.69 km 3 ·a -1 ,年均值为850.46 km 3 ·a -1 (214.07 mm·a -1 );3)影响中亚地区植被NPP和ET变化的气候因子主要为降水,温度影响相对较弱;4)吉尔吉斯斯坦和塔吉克斯坦植被生产力增长较快,哈萨克斯坦、乌兹别克斯坦和新疆较为稳定,土库曼斯坦植被生产力出现下降现象。

1999

0.0

任继周, 胡自治, 张自和, 侯扶江, 陈全功. 中国草业生态经济区初探. 草业学报, 1999, 8(1): 12-22.

Ren J

, Hu Z

, Zhang Z

, Hou F

, Chen Q

Apreiminary discussion on grassland ecological-economic regions in China.

Acta Prataculturae Sinica, 1999, 8(1): 12-22. (in Chinese)

摘　要：根据生态条件的相似性 (尤其是水、热条件的相似性 )、草地类型和景观的相似性、草业系统生产层的结构和生产内涵的趋同性、草地生态系统与经济系统的内涵与外延的相似性、草业发展对策和关键技术的相似性和草业生产区域规划的组织与实施的空间可操作性 (即一定级别上行政区划界限的完整性 )等 6项原则 ,我国可划分为 7个草业生态经济区 :蒙宁干旱草原草业生态经济区、西北荒漠灌丛草业生态经济区、青藏高寒草业生态经济区、东北森林草业生态经济区、黄土高原—黄淮海灌丛草业生态经济区、西南岩溶山地灌丛草业生态经济区和东南常绿阔叶林—丘陵灌丛草业生态经济区。以自然条件和草业生产现状为基础 ,分区提出草业发展对策

... 草地NPP的研究对草地资源的合理利用,挖掘草地气候生产潜力,最大程度提高产量以及对草地农业生态系统中碳循环研究都具有指导意义^{[7,8,9,10,11]} ...

2007

0.0

2008

0.0

张伟科, 刘玉杰, 封志明, 孙小舟. 内蒙古天然草地生产潜力及其限制性研究. 草地学报, 2008, 16(6): 572-579.

Zhang W

, Liu Y

, Feng Z

, Sun X

A Study of rangeland productive potential and limiting factors in Inner Mongolia Autonomous Region.

ActaAgrestia Sinica, 2008, 16(6): 572-579. (in Chinese)

The rangeland productive potential research is advantageous to the reasonable use of rangeland resources.It gives full play to the rangeland productive potential and maximizes the output of grassland.There are some research models about it,such as climate productivity model,process model,and light energy use efficiency model.Against the six types of rangeland in Inner Mongolia Autonomous Region,established models were revised gradually according to solar radiation,air temperature,air humidity,soil fertility,and utilization status of rangeland resources,based on the meteorological data during 1980-2001 years,and the potential productivity range of rangeland resources in Inner Mongolia Autonomous Region was calculated using ArcGIS software at 1km x 1km grid level per ten days.The spatial distribution pattern of productive potential at each level was revealed.The main limiting factors of rangeland productive potential were found.The results show that the potential productivity of various rangeland types gradually decreased and the range of rangeland productive potential in the Inner Mongolia Autonomous Region was from 454 kg·hm -2 to 12323 kg·hm -2 .The spatial distribution trend declined from the southeast to northwest of the Inner Mongolia Autonomous Region.The limiting factors of productive potential were different from different regions and different types of rangeland.

研究构建了"光、温、水、土与草地利用"草地生产潜力5级订正模型,利用ArcGIS软件,以1 km×1 km栅格为单元,根据1980—2001年间气象观测资料,定量计算了对内蒙古6种天然草原的光合、光温、气候、土地和自然生产潜力,揭示了各级生产潜力的空间分布格局,并找出了天然草地生产力形成的主要限制因子。结果表明:从光合、光温、气候、土地到自然生产潜力,各种草地类型的生产潜力逐级降低;内蒙古草原生产潜力的分布范围在454~12323 kg/hm 2 ;空间分布趋势是由东南向西北递减;不同地域、不同草地类型生产潜力的主导限制因子不同。

2015

0.0

潘竟虎, 文岩. 中国西北干旱区植被碳汇估算及其时空格局. 生态学报, 2015, 35(23): 7718-7728.

Pan J

, Wen

Estimation and spatial-temporal characteristics of carbon sink in the arid region of northwest China.

Acta Ecologica Sinica, 2015, 35(23): 7718-7728. (in Chinese)

Global warming caused by greenhouse gas emissions has had a profound impact on human survival and development. Consequently, this phenomenon has received widespread attention from the international community. Vegetation can absorb greenhouse gases CO 2 , and has a huge carbon sink function, so it has an irreplaceable role in slowing global warming. The carbon sink capacity of vegetation has a significant impact on regional and global climate change. Carbon emissions are undoubtedly enormous in the mid and high latitudes of the Northern Hemisphere, so studies on terrestrial ecosystem carbon dynamics and spatial patterns in the arid region of northwest China may provide an accurate assessment how China contributes towards mitigating global climate change and CO 2 emission reduction. The net primary productivity (NPP) and heterotrophic respiration ( R H ) in the arid region of northwest China were calculated by using MODIS images, meteorological data, and a vegetation type map, in combination with an improved CASA model and soil microbial respiration model. The NPP and R H were then used to estimate net ecosystem productivity (NEP) and vegetation carbon sink from 2001 to 2012. Spatial-temporal characteristics and the reasons for NPP and carbon sink variation in the arid region of northwest China were analyzed. The results show that research methods used in this paper were able to quickly extract ecosystem net primary productivity and carbon sink for the northwest arid region. The methods used are efficient, convenient, and practical for large scale carbon balance and carbon cycling studies in this region. Comparison indicated small gaps between simulated and measured site values. The overall difference in the spatial distribution between simulated values and MODIS NPP products is also small, and the volatility of the analog value is less than the value of MODIS NPP products. NPP in the study area showed strong seasonal variation. The maximal NPP value was obtained in July, while the minimum value was obtained in December. In the 12 study years, annual averages of NPP changed minimally. Average carbon sinks showed fluctuating in the 12 years, but increased in general, overall. The carbon sink mean changed from a minimum of 609.04 gC -1 m -2 a -1 in 2006 to a maximum of 648.02 gC -1 m -2 a -1 in 2012. The change in mean carbon sink was less than 39 gC -1 m -2 a -1 , with a standard deviation of 11.68. Annual maximum carbon mainly occurred in May, June, and July. Carbon sink fluctuated, but showed an overall upward trend in the northwest arid region between 2001 and 2012. Carbon sink in this region gradually increased from West to East, with Eastern > West > Central. The carbon sink capacity of different natural areas was quite different. The largest carbon sink capacity was recorded in the grassland area of West Liaohe River Basin, while the smallest was recorded in the warm temperate desert region of the Tarim Basin. The annual maximum carbon sink mainly occurred from May to July. Carbon sink was ranked in the order of coniferous forest > farmland > shrubs > broad-leaved forest > grassland > desert steppe.

通过修正的CASA模型估算2001-2012年间西北干旱区陆地生态系统的净第一性生产力(NPP),并结合土壤微生物呼吸方程,计算出12a的净生态系统生产力(NEP),分析了植被碳汇的时空变化规律。结果表明:研究区的NPP表现出很强的随季节变化的规律,全年7月份NPP为最高值,12月为最低值,12 年间NPP的年均值变化不大。2001-2012 年研究区的植被碳汇在波动变化中有所增加,其中2006年的碳汇平均值最小,为609.04 gC m -2 a -1 ,2012年最大,为648.02 gC m -2 a -1 ;年内碳汇的最大值主要出现在5-7月;碳汇能力由大到小的植被类型为针叶林 > 农田 > 灌丛 > 阔叶林 > 草原 > 荒漠草原。研究区多年平均碳汇量呈现自西向东逐渐增加的规律,西辽河流域草原区的NPP和碳汇平均值最大,塔里木盆地暖温带荒漠区最小。

2015

0.0

刘海江, 尹思阳, 孙聪, 彭福利, 周澎. 2000-2010年锡林郭勒草原NPP时空变化及其气候响应. 草业科学, 2015, 32(11): 1709-1720.

Liu H

, Yin S

, Sun

, Peng F

, Zhou

Temporal and spatial variation of net primary productivity (NPP) and its responses with climatic changes in the Xilingol grassland from 2000 to 2010

Pratacuhural Science, 2015, 32(11): 1709-1720. (in Chinese)

Using MODIS MOD17A3 Net Primary Productivity (NPP) data and meteorological data, we analyzed the temporal and spatial variation of NPP, inter-annual changes of climatic factors and the correlative relationship between NPP and climatic factors in Xilingol grassland from 2000 to 2010. The NPP of the Xilingol grassland varied from 0 to 0.5 kg C·m -2 which decreased from east to west. From 2000 to 2010, the NPP fluctuated annual that increased in generaland evenly distributed. The variations of climatic factors in typical and desert grassland were similar. The cumulative average temperature, average relative humility and cumulative sunshine duration in April to August had a downward trend, while the average wind speed had an increasing trend. The cumulative precipitation hadan increasing trend in desert grassland, but had a slight decreasing trend in typical grassland. For most climatic factors, they had more dramatic fluctuations in typical grassland than in desert grassland. For the two types of grassland in the study area, the grassland NPP has very significantly negative correlation ( P <0.001) with cumulative average temperature and average daily minimum temperature in April to August, and had slight negative correlation with cumulative sunshine duration and average wind speed, while had strong positive correlation ( P <0.001) with cumulative precipitation and average relative humility. In conclusion, the typical grassland had stronger response ability to the changes of climatic factors than the desert grassland.

利用MODIS MOD17A3植被初级生产力数据产品及地面气象观测数据,研究分析了2000-2010年锡林郭勒盟草原NPP的时空变化特征、各气候因子的年际变化特征及NPP与气候因子的相关关系。结果表明,锡林郭勒盟草原NPP的分布由东向西逐渐减小,值大多分布在0~0.5 kg C·m -2 ;2001-2010年NPP呈现波动变化,整体呈增加趋势,空间分布上更加趋于均匀分布;2000-2010年,研究区内典型草原和荒漠草原各气候因子的变化趋势大致相同,4-9月累计平均气温、平均相对湿度和累计日照时数呈减小趋势,平均风速呈增加趋势,累计降水量典型草原呈轻微减少趋势,荒漠草原呈增加趋势,趋势斜率分别为-0.026和1.044 5,典型草原大部分气候因子的波动程度大于荒漠草原;研究区内两种类型的草原的NPP均与4-9月累计平均气温、平均日最低气温有较强的负相关关系(显著水平分别为 P< 0 . 001和 P <0.01),与累计降水量、平均相对湿度有较强的正相关关系(显著水平为 P <0.01),与4-9月累计日照时数、平均风速呈负相关关系但相关关系较弱,荒漠草原对气候因子变化的响应总体不如典型草原敏感。

... 因为草原生态环境的天然脆弱性以及其对气候变化响应较为敏感,温度和水分是影响草地生态系统演替重要气候驱动因子,同时也是影响草地生产力的关键因素和估算草地生态环境及NPP的重要指标^{[11,12,13,14]} ...

2011

0.0

杜加强, 舒俭民, 张林波, 郭杨. 黄河上游不同干湿气候区植被对气候变化的响应. 植物生态学报, 2011, 11: 1192-1201.

Du J

, Shu J

, Zhang L

, Guo

Responses of vegetation to climate change in the headwaters of China’s Yellow River Basin based on zoning of dry and wet climate.

Acta Phytoecologica Sinica, 2011, 11: 1192-1201. (in Chinese)

Aims Precipitation and temperature are considered the limiting factors to vegetation growth in arid and cold areas, respectively. Our objective was to study the trends in vegetation cover and productivity and their relationships with prevailing hydrothermal factors in order to better understand climatic constraints on regional vegetation dynamics. Methods We zoned dry and wet climates using daily meteorological data from 1959 to 2008 at 16 locations in the headwaters of the Yellow River Basin to calculate the ratio of precipitation to evapotranspiration estimated with the FAO Penman-Monteith model. Based on this zoning, the temporal dynamics of vegetation and changes in climate were analyzed using the normalized difference vegetation index ( NDVI ) obtained from the NASA AVHRR sensor (1982–2006) and the GLOPEM net primary productivity ( NPP ) (1981–2000) and corresponding annual meteorological data. Then we developed the relationships between NDVI and NPP and climatic factors. Important findings The region studied is semi-humid in the southeast and semi-arid elsewhere, with a boundary nearly matching the 450 mm rainfall contour. The weather became wetter and especially warmer in most parts of the region during 1981–2006. The regional average NDVI and NPP markedly increased in semi-humid areas and slightly increased in semi-arid areas. Overall, NDVI had a significantly positive correlation with mean annual air temperature and a mainly negative correlation with mean annual precipitation in most semi-humid areas. The most important factor influencing NDVI was heat. In contrast, the key climatic factor affecting vegetation changes in the semi-arid areas was water, the relationship between NDVI and precipitation was strong and vegetation was more sensitive to changes in precipitation. The impact of climate change on NPP was similar to that on NDVI . Findings suggest that the responses of vegetation to climate change depend in part on the hydrothermal conditions of the region, and the zoning of dry and wet climate illustrates the spatial difference of vegetation feedback to climate change.

研究气候变化背景下植被变化趋势及其与水热因子的关系, 对于黄河源区的生态恢复和生态建设具有重要意义。采用基于FAO Penman-Monteith的降水蒸散比来描述区域的干湿状况, 划分了黄河上游地区的干湿气候区。在此基础上, 利用AVHRR归一化植被指数( NDVI )和GLOPEM净初级生产力( NPP )数据集和同期的气候资料, 分析了黄河上游植被覆盖、植被生产力和气候变化的趋势, 探讨了不同干湿气候区影响植被变化的主要气候因子。结果表明, 研究区域东南部为半湿润气候区, 其余为半干旱气候区, 干湿气候分界线与450 mm降水等值线较接近; 1981–2006年区域气候趋于干暖化, 尤其是气温的升高趋势明显; 半湿润地区 NDVI 和 NPP 显著增加, 半干旱地区略有增加; 半湿润地区的 NDVI 多与气温显著正相关, 与降水量的相关性较弱, 气温是植被生长的主要气候制约因素; 半干旱地区的 NDVI 则与降水量的正相关性更强, 对降水量的变化较为敏感。 NPP 对气候变化的响应模式与 NDVI 相似。植被对气候变化的响应部分依赖于研究区域所具备的水热条件, 干湿气候划分有助于更好地解释植被对气候变化响应的空间差异。

2009

0.0

高浩, 潘学标, 符瑜. 气候变化对内蒙古中部草原气候生产潜力的影响. 中国农业气象, 2009, 30(3): 277-282.

Gao

, Pan X

, Fu

Influence of climate change on potential climate productivity in grassland of central Inner Mongolia.

Chinese Journal of Agrometeorology, 2009, 30(3): 277-282. (in Chinese)

Based on the climate date in 1961-2007 in the grassland of the Central Inner Mongolia,the response of the potential climate productivity to the climate change was analyzed,by using the Miami model and Thornthwaite Memorial model. The climatic factors affected the productivity were discussed. The results showed that the potential climate productivity in the grassland of the Central Inner Mongolia had the consistent difference with the geographical distribution and the precipitation distribution. The potential climate productivity was with 3000-7000kg·ha-1each year,which distributed in the different grassland types from high to low in following order:steppe,agro-pastoral ecotone,desert steppe,steppe desert. The climatic utilization was by 23.8%-48.2%,which varied in the different grasslands. The precipitation was the key climatic factor limited the potential climate productivity and actual productivity by analyzing experimented date and climate productivity modelling. Both temperature and precipitation increase could enhance the potential climate productivity. The impact of temperature and precipitation change on the potential climate productivity varied in the different grassland. The potential climate productivity increased or decreased by 6.75-29.07kg ·ha-1 each year as the temperature increased or decreased by 1℃,while the potential climate productivity increased or decreased by 0.83-1.86kg·ha-1each year as the precipitation increased or decreased by 1mm. Under the background of drier and warmer tendency,the increasing amount of potential climate productivity with temperature increase was less than decreasing amount with evapotranspiration increase. Therefore,climate drying and warming in the future will lead to potential climate productivity decrease. The more obviously the potential climate productivity was limited by precipitation,the more significantly the potential climate productivity decreased.

根据内蒙古中部草原各样点47a的气候数据,基于Miami和Thornthwaite Memorial气候模型,分析研究区域不同草原类型草地生产潜力和影响气候生产潜力的气候驱动力。结果显示,内蒙古中部草原的气候生产潜力由东向西表现出与地理分布和降水量分布趋势一致的差异性,农牧交错带草地>典型草原>荒漠草原>草原化荒漠,其气候生产潜力在3000～7000kg.hm-2.a-1。研究区域的气候资源利用率在23.8%～62.3%,不同草原存在一定的差异性。分别采用草原样方取样实际产量数据、气候数据和气候生产力模型数据计算分析表明:与温度相比,降水量是影响研究区域牧草产量和气候生产潜力的主要气候驱动力,温度与降水对草原气候生产潜力都具有正效应,不同草原类型温度与降水变化对气候生产潜力的影响有差异性。温度每升高或降低1℃,草地气候生产潜力升高或降低6.75～29.07kg.hm-2.a-1,降水量每升高或降低1mm,草地气候生产潜力升高或降低0.83～1.86kg.hm-2.a-1。未来气候"干暖化"的趋势下,研究区域温度升高增加的气候生产潜力作用小于由蒸散量增加引起的减产作用,因而导致草地气候生产潜力下降,受水分限制作用越明显的草原,其气候生产潜力下降的趋势越显著。

2013

0.0

... 根据前期研究表明,新疆草地植被NPP与降水的相关性显著^[15],因此,气象数据的精准性会很大程度地影响草地植被NPP的估算 ...

2015

0.0

殷刚, 陈曦, 塔西甫拉提·特依拜, 邵华, 白磊, 胡增运, 张弛, 徐婷. 气候模式同站点插值外推气象数据的比较. 地理研究, 2015, 34(4): 631-643.

Yin

, Chen

, Tiyip·Tashpolat, Shao H, Bai L, Hu Z Y, Zhang C, Xu T. A comparison study between site-extrapolation-based and regional climate model-simulated climate datasets. Geographical Research, 201, 34(4): 631-643. (in Chinese)

Regional Climate Model (RegCM) simulations, which is based on the fundamental physical and metrological mechanisms, could produce high-resolution climate dataset, without being limited by the availability of meteorological stations in Central Asia. In order to analyze the climate change in Xinjiang from 1958 to 2001, this study used the RegCM model to downscale the ERA40 and NCEP/NCAR reanalysis datasets to a 40-km resolution, and compared the simulation results with three widely used extrapolation datasets (CRU, WM and APHRO). All datasets indicated increased temperature in Xinjiang, increased precipitation in southern Xinjiang, and decreased precipitation in the Tianshan mountainous areas. All datasets except for the APHRO interpolated data indicated increased precipitation in northern Xinjiang. Our analysis showed similar spatial patterns in temperature and precipitation between the RegCM simulated and the extrapolation datasets. However, the simulated regional mean temperature was -3℃ lower than that of the extrapolated datasets. The simulated precipitation in the Tianshan mountainous areas was about twice the value of the extrapolated datasets. Because 73% of the meteorological stations in the study located at the low-mountain areas or the desert plains were in relatively hot and dry climate regimes, extrapolation datasets based on observations at these stations tended to overestimate temperature and underestimate precipitation. Compared with the extropolation method, regional climate modelling considers the detailed topography/landsurface characteristics in the study region at meso-/micro-scales, and is capable to reflect the spatial variation of major climatological elements with higher precision. However, due to limited sparse field observations and a lack of high-resolution remote-sensing-based climate datasets, we are currently unable to fully evaluate the accuracy of the model simulated climate datasets in central Asia, especially in the mountainous areas.

1. State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, CAS, Urumqi 830011, China 2. Xinjiang University, Urumqi 830046, China 3. University of Chinese Academy of Sciences, Beijing 100049, China 4. The Yili Weather Bureau in Xinjiang, Yining 835000, Xinjiang, China

在气象站稀疏的中亚荒漠地区采用基于大气物理机制的区域气候模式,可获得高分辨率格点气象资料进行气候变化研究。针对中亚地区1958-2001年的气候变化,采用RegCM区域气候模式对ERA40和NCEP/NCAR两套气象再分析数据进行动力降尺度至40 km,并将结果同三套基于气象站点插值外推的格点数据（CRU、WM和APHRO）进行比较。所有数据一致表明,1960年代以来新疆地区的气温显著增加,南疆地区降水增加、天山山区降水减少。除APHRO外,数据都表明北疆地区降水呈增加趋势。RegCM模拟的气温和降水数据与站点外推数据空间分布格局基本一致;但RegCM数据年平均气温低于站点外推数据,RegCM数据在新疆山区的年降水量是站点外推数据年降水量的1.3倍。由于研究区内73%的气象站点分布在中山带以下的干热气候区,站点外推数据可能低估山区降水并高估该区域气温。与站点插值外推的格点数据相比,区域气候模式具有能细致描述区域内中小尺度的地形/下垫面特征、更精确反映气象要素空间变异格局的能力。但因为缺乏足够的地面观测以及高精度遥感反演气象数据,当前尚无法全面评估区域气候模式在中亚地区尤其是山区的模拟精度。

... 随着气候变化研究的日益深入,如何基于有限的、分布不均的站点气象观测数据获得某一地区的气候要素时空分布情况,从而提高降水、气温空间模拟的精度已成为气候变化领域的热点问题^[16,17,18] ...

2014

0.0

王丽娜. 气象要素空间插值算法的研究及其应用. 重庆: 重庆理工大学硕士学位论文, 2014.

Wang L

Algorithm research and application of meteorological spatial interpolation. Master’s Thesis.

Chongqing: Chongqing University of Technology, 2014. (in Chinese)

气象要素的空间插值方法为每个研究区域内的栅格提供气象要素数据，将空间上离散的气象数据转换为连续的曲面数据，以便对气象分布进行建模研究。然而，在现有的气象要素空间插值方法中，并没有一种普遍最优的插值方法可以适合所有的气象要素和地理条件。目前亟待研究解决的问题就是——根据研究区域内气象台站的数目、区域空间的分布情况和特定的气象要素等具体条件选择适合当前的最优空间插值方法，以提高插值精度和效率。该文在对现有的空间插值方法研究基础上提出了基于时间序列的时空插值算法和自适应离散点插值算法。首先，该文对空间插值算法进行了改进研究，结合时间序列模型提出了时空混合插值算法：该算法更符合气象要素的时空特性，从源头上解决了由于各种不可抗力因素（如仪器故障，传输线路故障等）造成的气象站点实时数据缺失等问题，采用重庆市900多个气象站近一年的观测数据与传统空间插值方法进行对比研究，证实了该算法的可行性。其次，为了获取高精度的气象台站测量盲区关注点的实时插值数据，结合时空混合插值算法所得到的气象台站缺失的实时数据，提出了自适应离散点插值算法：该插值算法弥补了现有空间插值算法只做统计使用的片面性，提出了根据区域气象台站的数目、区域空间分布特征和待研究气象要素的特点等属性选择相对最优的空间插值方法，并通过重庆市900多个气象站近一年的观测数据，以294个重点变电站为关注点完成了气象要素空间离散插值方法的对比验证，得出每个关注点的最优插值方案，给关注点提供高精度的实时气象插值数据。最后，该文将基于时间序列的时空插值算法和自适应离散点插值算法应用于重庆市电网气象灾害实时预警系统中，通过一系列实时数据测试了算法的可用性和可行性，结果证明了论文的研究是可行的、正确的。

2012

0.0

... 与反距离加权法、径向基函数法、协克里格方法相比,普通克里格法对新疆全疆降水空间分布进行插值的计算精度最高^[19] ...

0.0

... 基于ANUSPLIN软件的局部薄盘光滑样条法对东北地区气温序列进行插值的结果最优^[20] ...

2014

0.0

... 2%,居全国第3位^[21,22,23] ...

1993

0.0

... 2%,居全国第3位^[21,22,23] ...

0.0

... 2%,居全国第3位^[21,22,23] ...

0.0

... 局部薄盘光滑样条法是在薄盘光滑样条法的基础上扩展而来,与薄盘光滑样条法不同的是,除普通的样条自变量以外,局部薄盘光滑样条法允许引入线性协变量子模型,例如海拔与气温之间的相关性^[24] ...

2014

0.0

杨红飞, 刚成诚, 穆少杰, 章超斌, 周伟, 李建龙. 近10年新疆草地生态系统净初级生产力及其时空格局变化研究. 草业学报, 2014, 23(3): 39-50.

Yang H

, Gang C

, Mu S

, Zhang C

, Zhou

, Li J

Analysis of the spatio-temporal variation in net primary productivity of grassland during the past 10 years in Xinjiang.

Acta Prataculturae Sinica, 2014, 23(3): 39-50. (in Chinese)

Dynamic monitoring of regional NPP (net primary productivity) has important significance for research on global change. The NPP of Xinjiang grassland from 2001 to 2010 was estimated using an improved light use efficiency model based on MODIS-NDVI, land use classification data and meteorological data. Spatial-temporal variation features of grassland NPP from 2001 to 2010 in Xinjiang were studied and analysed. The spatial distribution of NPP in Xinjiang grassland was constrained by the regional hydrothermal conditions. Grassland types were generally distributed as alpine and sub-alpine meadow, plain grassland, meadow, desert grassland, alpine and sub-alpine grassland from north to south. The grassland NPP reduced from 395 g C/(m 2 ·a) to near 0 g C/(m 2 ·a) and 10-year average total NPP of Xinjiang grassland was 56.47 Tg C. Compared with other grassland types, mean NPP of meadow was the highest (155.29 g C/m 2 ·a), while mean NPP of desert grassland was the lowest (57.68 g C/m 2 ·a). The overall level of mean NPP was meadow>alpine and sub-alpine meadow>plain grassland>alpine and sub-alpine grassland>desert grassland. The overall level of grassland NPP in Xinjiang was rather low, where alpine and sub-alpine meadow, plain grassland and meadow belonged to lower productive ecosystems, and desert grassland, alpine and sub-alpine grassland belonged to the lowest productive ecosystems. On the main grasslands in Xinjiang, the NPP from June to August occupied 63.17% of the whole year. The monthly NPP in different grasslands changed differently but all peaked in July. Compared with other types, NPP of alpine and sub-alpine meadow increased more quickly in the first seven months, while alpine and sub-alpine grassland were the slowest. The decrease of meadow NPP was quicker than those of other grassland types in the last five months, while desert grassland was the slowest. With the exception of meadow, the mean NPP of the other four grassland types showed a downward trend from 2001 to 2010 in Xinjiang. Total NPP of grassland in Xinjiang reached the maximum (60.21 Tg C/a) in 2007, and dropped to the minimum (53.41 Tg C/a) in 2006. During the past 10 years, the grassland NPP in Xinjiang showed a great annual fluctuation but with an overall reduction trend.

基于2001-2010年遥感监测和气象数据,采用CASA(Carnegie-Ames-Stanford Approach)模型模拟分析新疆地区草地植被净初级生产力(NPP)及其时空变化特征。结果表明,新疆草地植被NPP空间分布特征受区域水热条件的制约,草地植被大体上由北向南依次出现高山与亚高山草甸、平原草地、草甸、荒漠草地和高山与亚高山草地,其NPP也逐渐由395 g C/(m 2 ·a)减少到接近0 g C/(m 2 ·a)。10年间,新疆草地NPP总量平均值为56.47 Tg C。新疆不同草地类型的NPP存在较大差异。其中,草甸的平均NPP最高,为155.29 g C/(m 2 ·a);荒漠草地的平均NPP最低,为57.68 g C/(m 2 ·a);总体表现为草甸>高山与亚高山草甸>平原草地>高山与亚高山草地>荒漠草地;新疆地区草地植被NPP整体水平较低,其中,高山与亚高山草甸、平原草地和草甸属于较低生产力的生态系统;而荒漠草地和高山与亚高山草地则属于最低生产力的生态系统。新疆主要草地植被6-8月NPP占全年NPP的63.17%。不同草地类型的平均NPP月际变化差异较大,均在7月达峰值。前7个月平均增长速度最快的是高山与亚高山草甸,最慢的是高山与亚高山草地;后5个月平均下降速度最快的是草甸,最慢的是荒漠草地。除草甸呈增长趋势外,其他4种草地类型的平均NPP总体上表现出一定的下降趋势,其中,平原草地的平均NPP下降速率最快。全区草地植被NPP总量在2007年达最高值,为60.21 Tg C/a,最低值出现在2006年,为53.41 Tg C/a。草甸是新疆5种草地类型中NPP总量唯一呈逐渐增长的草地类型,而其他4种草地类型均呈下降趋势,其中平原草地的NPP总量下降速率最快。近10年来,新疆全区草地植被总NPP的年际变化较大,有进一步下降趋势。

... 5 草地NPP的估算相关研究表明,CASA模型比较适用于新疆地区草地NPP估算研究^[25],因此,本研究采用朱文泉等^[26,27]改进的CASA模型 ...

2005

0.0

朱文泉. 中国陆地生态系统植被净初级生产力遥感估算及其与气候变化关系研究. 北京: 北京师范大学博士学位论文, 2005.

Zhu W

Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing and its relationship with global climate change. PhD Thesis.

Beijing: Beijing Normal University, 2005. (in Chinese)

本文主要运用地理信息系统和遥感手段，利用AVHRR多时相遥感数据、气象数据及相关的植被生理生态统计资料，在建立陆地植被NPP遥感估算模型的基础之上，重建了中国陆地生态系统1982～2000年不同土地覆盖下NPP年际、年内变化的时空序列及演变模式；分析了过去19年来中国陆地生态系统NPP对区域温度、降水变化的响应方式及反馈机制，初步揭示了影响NPP变化的气候驱动力因子及机制，获得了以下主要结论。1NPP遥感估算模型本文所构建的NPP遥感估算模型体现了三方面的特色：(a)水分胁迫因子的计算更为简便，所反映的空间分布趋势也与实际情况比较符合；(b)在估算植...

... 5 草地NPP的估算相关研究表明,CASA模型比较适用于新疆地区草地NPP估算研究^[25],因此,本研究采用朱文泉等^[26,27]改进的CASA模型 ...

2007

0.0

朱文泉, 潘耀忠, 张锦水. 中国陆地植被净初级生产力遥感估算. 植物生态学报, 2007, 31(3): 413-424.

Zhu W

, Pan Y

, Zhang J

Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing.

Acta Phytoecologica Sinica, 2007, 31(3): 413-424. (in Chinese)

Aims Net primary productivity ( NPP ) is a key component of the terrestrial carbon cycle. Model simulation is commonly used to estimate regional and global NPP given difficulties to directly measure NPP at such spatial scales. A number of NPP models have been developed in recent years as research issues related to food security and biotic response to climatic warming have become more compelling. However, large uncertainties still exist because of the complexity of ecosystems and difficulties in determining some key model parameters. Methods We developed an estimation model of NPP based on geographic information system (GIS) and remote sensing (RS) technology. The vegetation types and their classification accuracy are simultaneously introduced to the computation of some key vegetation parameters, such as the maximum value of normalized difference vegetation index (NDVI) for different vegetation types. This can remove some noise from the remote sensing data and the statistical errors of vegetation classification. It also provides a basis for the sensitivity analysis of NPP on the classification accuracy. The maximum light use efficiency ( LUE ) for some typical vegetation types in China is simulated using a modified least squares function based on NOAA/AVHRR remote sensing data and field-observed NPP data. The simulated values of LUE are greater than the value used in the CASA model and less than the values simulated with the BIOME-BGC model. The computation of the water restriction factor is driven with ground meteorological data and remote sensing data, and complex soil parameters are avoided. Results are compared with other studies and models. Important findings The simulated mean NPP in Chinese terrestrial vegetation from 1989-1993 is 3.12 Pg C (1 Pg=10 15 g). The simulated NPP is close to the observed NPP , and the total mean relative error is 4.5%for 690 NPP observation stationsdistributed in the whole country. This illustrates the utility of the model for the estimation of terrestrial primary production over regional scales.

该文在综合分析已有光能利用率模型的基础上，构建了一个净初级生产力( NPP )遥感估算模型，该模型体现了3方面的特色：1)将植被覆盖分类引入模型，并考虑植被覆盖分类精度对 NPP 估算的影响，由它们共同决定不同植被覆盖类型的归一化植被指数( NDVI )最大值；2)根据误差最小的原则，利用中国的 NPP 实测数据，模拟出各植被类型的最大光能利用率，使之更符合中国的实际情况；3)根据区域蒸散模型来模拟水分胁迫因子，与土壤水分子模型相比，这在一定程度上对有关参数实行了简化，使其实际的可操作性得到加强。模拟结果表明，1989～1993年中国陆地植被 NPP 平均值为3.12 Pg C (1 Pg=10 15 g)， NPP 模拟值与观测值比较接近，690个实测点的平均相对误差为4.5%；进一步与其它模型模拟结果以及前人研究结果的比较表明，该文所构建的 NPP 遥感估算模型具有一定的可靠性，说明在区域及全球尺度上，利用地理信息系统技术将遥感数据和各种观测数据集成在一起，并对 NPP 模型进行参数校正，基本上可以实现全球范围不同生态系统 NPP 的动态监测。

... 5 草地NPP的估算相关研究表明,CASA模型比较适用于新疆地区草地NPP估算研究^[25],因此,本研究采用朱文泉等^[26,27]改进的CASA模型 ...

2010

0.0

钱永兰, 吕厚荃, 张艳红. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估. 气象与环境学报, 2010, 26(2): 7-15.

Qian Y

, Lyu H

, Zhang Y

Application and assessment of spatial interpolation method on daily meteorotogica1 elements based on ANUSPLN software.

Journal of Meteorology and Environment, 2010, 26(2): 7-15. (in Chinese)

Meteorological elements are the basic data for the study on resources, environment, disaster and global change fields, and their gridding data become more and more important for the study at large scale. The daily air temperature and precipitation were interpolated by spline interpolating method from ANUSPLIN software based on the data from 667 weather stations of China from 1961 to 2006 in order to get the gridding data, and the interpolating results were validated by the data from other 1667 dense observation stations. The interpolating results were compared with those data based on intense distance weight method and ordinary kriging method. It indicates that the errors within 2.0 ℃ for daily average air temperature account for 92.0%, and those within 2.0 ℃ and over 5.0 ℃ are 75.0% and 0.9%, respectively. The mean absolute error is 0.8℃. On the other hand, the errors within 5.0 mm and 10.0 mm for daily precipitation account for 75.0% and 85.0%, respectively, and the mean absolute error is 6.4 mm. The relationship between the error ranges of gridding precipitation and observation values of precipitation are positive, and interpolating accuracy decreases for local strong precipitation, which maybe result from the insufficient observation values. Furthermore, the interpolating accuracy for air temperature is higher in summer than in winter, while that for precipitation is higher in winter than in summer. The validation results indicate that the accuracy of gridding data based on spline interpolation method of ANUSPLIN software is higher than that based on intense distance weight method and ordinary kriging method. It also indicates that more observation data and finer resolution DEM can improve the accuracy of the spline interpolation method of ANUSPLIN software.

气象要素是资源、环境、灾害以及全球变化等领域研究的数据基础，格点化数据在未来研究应用中显得日益重要。本文基于中国境内667个基本和基准地面气象观测站点的基本气象资料，使用ANUSPLIN专用气候插值软件对1961-2006年逐日气温、降水进行插值，并利用未参与插值的全国1667个加密站点对插值结果的准确性进行检验，同时与反向距离权重法和普通克吕格法等插值方法的结果进行对比。结果表明，利用667个站点使用ANUSPLIN软件进行逐日平均气温插值有92.0%的误差在2.0℃以内，75.0%的误差在1.0℃以内，0.9%的误差在5.0℃以上，平均绝对误差为0.8℃；对逐日降水进行插值，75.0%的误差小于5.0mm，85%的误差小于10.0mm，平均绝对误差为6.4mm，误差大小与降水量呈现出正相关性，对局地强降水的插值效果不好,这可能与参与局部拟合插值的样本数太少有关；同时，夏季的温度插值误差小于冬季，而冬季的降水误差小于夏季。将ANUSPLIN的局部薄盘样条插值结果分别与反向距离权重法和普通克吕格法的插值结果进行对比，显示ANUSPLIN软件的插值误差最小。结果同样表明，适当增加站点数量和提高DEM精度可进一步提高ANUSPLIN软件的插值精度。

... 3 讨论与结论空间内插方法是气象要素区域平均过程的基础,本研究表明,基于ANUSPLIN插值方法的精度最高,钱永兰等^[28]研究表明,与反距离权重法和克里格法进行逐日气象要素插值的结果进行对比,ANUSPLIN软件的插值误差最小 ...